
Samsung S23 Ultra Star-Trailing & Resolution
May 20, 2024
Astrophotography of star fields requires a basic understanding of star trailing, the streaking of star images in timed exposures
of a few seconds or longer. This of course is due to the rotation of the earth from west to east, causing the heavens to apparently
rotate from east to west. To obtain good astrophotographic images requires reasonably dark skies, a modest tripod (if the camera isn't large), an accurate sharp focus setting and short enough exposures to minimize
star trailing (unless of course one is trying to see star trails explicitly over an extended time exposure).
The handy well-known astrophotography "rule of 500" is useful as a starting benchmark and states that to minimize star trailing, the exposure should be:
tmin(sec) < 500/f_eq(mm)
where f_eq is the camera "equivalent focal length" which is typically quoted for modern smart phones.
For example my Samsung S23 Ultra has 4 cameras, with the 3 most useful for astrophotos having different f_eq values. The
rule of 500 for exposure values are shown here (without extra digital zoom):
- x1 (normal W camera) f_eq = 23mm tmin ~ 22sec
- x3 telephoto f_eq = 70mm tmin ~ 7 sec
- X10 periscope f_eq = 230 mm tmin ~ 2 sec
As a fundamental check on these numbers using only the camera sensor dimensions and the sensor field-of-view (FOV),
let's calculate the amount of star trailing expected for x3 camera and compare with the rule of 500 recommendation.
The x3 camera has a f_eq ~ 70mm. The S23 Ultra default camera photo setting uses a 12 MP "pixel binning of 16 fundamental pixels".
According to Samsung, the sensor dimensions are (in pixels) 16,384 x 12,288 (200M) but with 4x4 pixel binning,
the 4x4 "pixel" resolution in the lateral direction is 4/16,384 or 1/4096.
The full angular field width for the x3 camera as specified
(and measured) is about 28°. So the angular width subtended by a quad pixel (in the x or y direction, not diagonally) is, in arc seconds:
28x60x60/4096 = 25 ∠sec.
The x3 camera has a lens aperture diameter of ~ 3mm and so the limiting angular resolution according the the Dawe's diffraction limit: 116/diam(mm) is ~ 40 ∠sec, somewhat larger than 25 ∠sec subtended by one 4x4 pixel.
Converting from angular units, with a full 360° circle being 360x60x60 = 1,296,000 ∠sec
to time units, with a full 24 hr day being 24x60x60 = 86,400 sec in time,
the angular width of a quad pixel in terms of time is 24/360*25 = 25/15 ~ 1.7 sec.
So the image of a perfect star (which we see as moving an entire circle in the sky for stars on the celestial equator) will move
across one quad pixel in ~ 1.7 sec for the x3 telephoto camera. For realistic sensors, a margin for aperture diffraction and nonideal lens quality and of course viewing conditions,
a star image will likely be blurred over at least 2 or 3 quad-pixels. So a reasonable exposure time to expect star trailing to show in an image using
the x3 camera is ~ 4 sec. The example here assumes the moving star is on the celestial equator which appears to move
the most due to the earth's rotation. So this estimate of 4 sec is the worst case estimate for realistic hardware and focus
tightness. Note that the rule of 500 above states 7 sec, almost twice as long.
A careful measurement shown below of distinct star trails of fainter stars for the best/sharpest photograph with the 3x camera
I have taken in the region of Orion's belt (within 2° of the celestial equator) for an exposure of 15 sec (using Astromode
on the S23 Ultra) shows star trailing with length about 220∠sec and a trail width of ~ 50∠sec
consistent with the reasonable limit discussed above. The exposure (not adjustable in Astromode)
should be reduced to 1/4 (4 sec) to eliminate any visible trailing,
about half the rule of 500 value, to show perfectly sharp rounded star images.


The rule of 500 values apply better for stars well above
or below the celestial equator (say > +- 30°). Estimated times will scale inversely with the f_eq so
the x1 camera has a worst case time of 12 sec and the x10 camera will be ~ 1 sec, both about half of the rule of 500 suggested values.
The first table below shows the camera sensor field of views (FOV) for each of the 3 main lenses (without extra digital zoom) and the angle subtended by the quad-pixel for
each lens, the camera lens diameters and the fundamental diffraction limit (Dawe's limit) determined only by the lens aperture diameter. For the x1 W camera, the picture resolution is limited by the quad-pixel
size whereas for the x10 Periscope camera, the picture resolution is limited by the lens diffraction limit.
The second table below shows the effects of using the S23 Ultra cameras along with an 8x35 binocular. The angular
resolution achievable under ideal conditions (perfect optics and perfect seeing conditions) is increased
dramatically to about 3 ∠" :
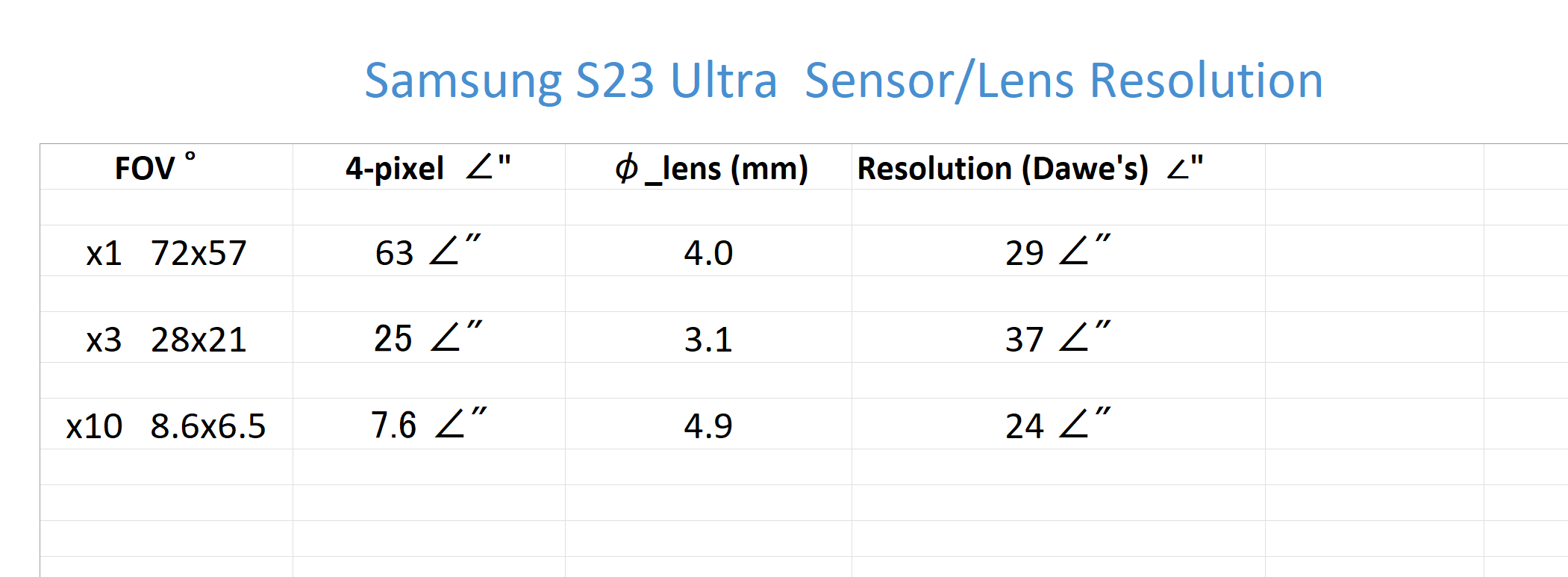

Note that for the x10 periscope camera, the image star size is limited by the diffraction limit
of the lens size (about 3 times bigger than the quad pixel angular resolution).
Assuming a realistic nonideal lens and typical reasonably good viewing conditions, one should
expect a resolution limit for observing double-stars to be about twice the theoretical case so
~ 40 ∠" for the x10 camera alone (for example ζ Lyrae) and ~ 7 ∠" with a 8x35mm binocular.
References:
1: Samsung Galaxy S23 Ultra Specs
2: Image Sensor Formats
3: Understanding Focal Length On Smartphone Cameras
4: Samsung Galaxy S23 Ultra Isocell HP2 Sensor
5: Samsung Galaxy S23 Wikipedia
6: Best Double Stars






